Sets Exist Therefore…
The Venn Diagram
Throughout this section, we will show operations in a visual form by showing Venn Diagrams of how the operations work. A Venn Diagram is a simple visualization for performing set operations that can assist in giving an intuition. The universe is represented as the entire image, and the sets are represented by bounded areas on the plane. You can use their crossings to show different operations.
Hopefully you remember Venn Diagrams from elementary school as ways of showing how something like book characters were different.
Example: Use a Venn Diagram to show how the characters Harry Potter and Luke Skywalker are similar and different.
Answer
No way I'm doing this for y'all, go ask a local middle schooler, feel free to switch it up with Rey instead of Luke or something.Compliment
If we were to look at some set $A$ that is a part of some universal set $U$ that we have previously defined ($U=\mathbb{Z}$ for example), then another question can be thought of not just all the items that are inside of our set $A$, but also all the items that are not inside of our set $A$. If we were to compile all these items that are not inside of $A$, then we would have a new set called the compliment of $A$.
Definition: The compliment of a set $A$, notated as $\bar{A}, A’, A^c$ is the set of all items in the universal set that are not inside of $A$. In set builder notation $$\bar{A}=\{x|x\in U, x\not\in A\}$$

For a real world example, if our universe was NJIT students, and our set $A$ was all students with a GPA of $4$, then $\bar{A}$ would be the set of all students with a GPA that is not $4$.
Example: Let $U=\{1,2,3,4,5\}$ and $A=\{1,2,3\}$, what is $\bar{A}$?
Answer
Since $4,5$ are the only items in the universe not in $A$, that means $$\bar{A}=\\{4,5\\}$$Set Union
Unlike the previous operation that only worked on one set, this next one works on two. If you can think of the compliment as similar to an inverse for logical variables, then the set union is akin to the logical OR. The set union takes in to sets and returns back the set that contains all the items that are in at least one of the sets.
Definition: The union of sets $A, B$, notated as $A\cup B$ is the set of all items in $A$ or $B$. In set builder notation $$A\cup B=\{x|x\in A\text{ or }x\in B\}$$
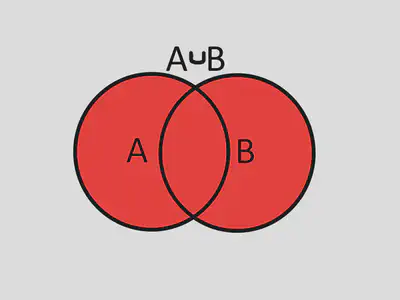
One way to create the set of all New York football teams would be to take the set of all NYC football teams, and all the Buffalo football teams (rip Bills and Giants 2022 Season lmfao) and union those two sets together
Example: Let $A=\{1,2,3,4,5\}$ and $B=\{5,6,7\}$, what is $A\cup B$?
Answer
$A\cup B=\{1,2,3,4,5,6,7\}$. As for all sets duplicates are only counted once.Notice that unlike the compliment, the union did not depend on our choice of universe. This will be the case for all future operations.
Set Intersection
What do you call the area that two roads connect to each other at, where often there is a traffic light? If you said an intersection, then you would be right! When it comes to sets, the intersection works the same way in that you have two sets, and you see where those two overlap. This is similar to a logical AND, but for sets.
Definition: The intersection of sets $A, B$, notated as $A\cap B$ is the set of all items in $A$ and $B$. In set builder notation $$A\cap B=\{x|x\in A\text{ and }x\in B\}$$
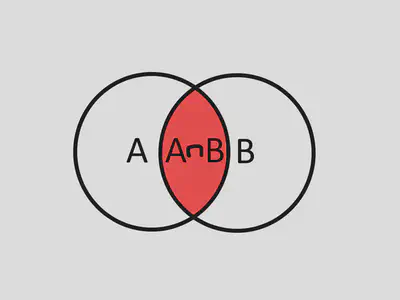
Example: Let $A=\{1,2,3,4,5\}$ and $B=\{5,6,7\}$, what is $A\cap B$?
Answer
$A\cap B=\{5\}$. As $5$ is the only item that appears in both setsWhat happens though if the items share nothing in common though? For example $A=\{\text{table}\}$ and $B=\{\text{chair}\}$? Then there is nothing in common and the intersection is $\varnothing$!
Definition: If two sets $A,B$ have no elements in common then they are disjoint or mutually exclusive, and $A\cap B=\varnothing$
Set Difference
Previously the operations had direct logical equivalent, however we are now going to work with a new operation that’s unique to sets. Suppose we got a list of all the students who were taking CS280 and CS288 at the same time, and put them into sets $C$ (for compiler) and $L$ (for Linux) respectively. Now say you wanted to send an email, but only to the students who were taking only CS288, and not CS280. Well we would need an operation to get rid of the overlap!
Definition: The difference of sets $A, B$, notated as $A-B$ is the set of all items in $A$ that are not in $B$. In set builder notation $$A-B=\{x|x\in A\text{ and }x\not\in B\},$$ which can also be written as $$A-B=A\cap\bar{B}.$$
Note that in this case it is not common that $A-B=B-A$. This is an example at the bottom of the page
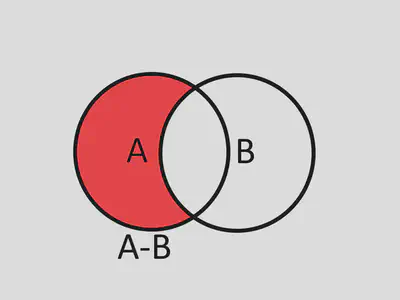
Example: Let $A=\{1,2,3,4,5\}$ and $B=\{5,6,7\}$, what is $A-B$?
Answer
$A-B=\{1,2,3,4\}$. This is because $5\in B$.Example: What is $\mathbb{N}-\mathbb{Z}_+$?
Answer
$\mathbb{N}$ is all the integers $\geq 0$ and $\mathbb{Z}_+$ is all integers $\geq 1$ so $$\mathbb{N}-\mathbb{Z}_+=\{0\}$$With set difference, we can also get a nice theorem to prove
Theorem Subset Difference Theorem: $A-B=\varnothing$ iff $A\subseteq B$.
Proof
We will first prove the forward direction that $A-B=\varnothing\implies A\subseteq B$.Since $A-B=\varnothing$ we know that by definition, there are no items inside of $A$ that are not inside of $B$, which means that if $x\in A$ then $x\in B$. This means that $A\subseteq B$.For the reverse direction that $A\subseteq B\implies A-B=\varnothing$, suppose that $x\in A$. Since $A\subseteq B$ then we know $x\in B$. By the definition of $A-B$ though we then know that $x\not\in A-B$, which is the case $\forall x\in A$. Therefore, $A-B=\varnothing$.Q.E.D.Symmetric Difference
The symmetric difference, like the set difference, is designed in terms of other operations. Unlike set difference though it is not used super frequently, rather it is occasionally used for the theorem that we will prove at the bottom of this section. Also, the notation is baller as fuck.
Definition: The symmetric difference of sets $A, B$, notated as $A\triangle B$ is defined to be $A\triangle B = (A-B)\cup (B-A) = (A\cup B) - (A\cap B)$
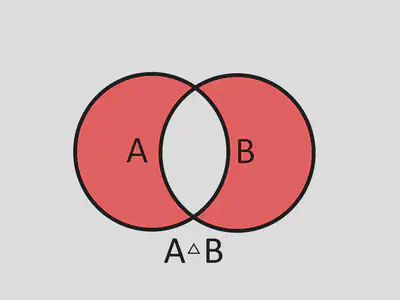
Example: Let $A=\{1,2,3,4,5\}$ and $B=\{5,6,7\}$, what is $A\triangle B$?
Answer
$A\triangle B=\{1,2,3,4,6,7\}$. This is because $5\in B,A$.The main purpose of the symmetric difference though is for use in the following theorem.
Theorem Difference Equality Theorem: $A\triangle B=\varnothing$ iff $A=B$.1
Proof
We will first prove the forward direction that $A\triangle B=\varnothing\implies A=B$.Since $A\triangle B=(A-B)\cup (B-A)=\varnothing$, we know that $(A-B)=\varnothing$ and $(B-A)=\varnothing$, as otherwise the symmetric difference would not be empty. Per the Subset Difference Theorem, we know that this means that $A\subseteq B$ and $B\subseteq A$ which is the definition of $A=B$For the reverse direction $A=B\implies A\triangle B=\varnothing$, we know that $A=B$ implies $A,B$ are subsets of each other, and by the Subset Difference Theorem above, we can say then that $$A\triangle B=(A-B)\cup (B-A)=\varnothing\cup\varnothing = \varnothing$$Q.E.D.Example Problems
Use these problems to test your proof skills with sets
Theorem: $A\cup B = \varnothing$ iff $A=\varnothing$ and $B=\varnothing$
Theorem: $A-B=B-A$ iff $A=B$
I am making up names for these theorems to reference later, don’t use these to look up cause they don’t have names. ↩︎